Marco Devillers
Eager Combinator Rewriting
I got some questions on how the Egel interpreter evaluates terms. The operational semantics of the eager combinator rewrite system I use is embarrassingly facile and trivial to explain with two pictures, so here goes.
Term evaluation
Say, you have a term language where you want to rewrite an expression consisting of combinators. In Egel’s case, each combinator is either a constant or coincides with a collection of rewrite rules, therefore, corresponds to a procedure or some code. Below, the graphical representation of the term “F (G 3) (H 2 7)”.
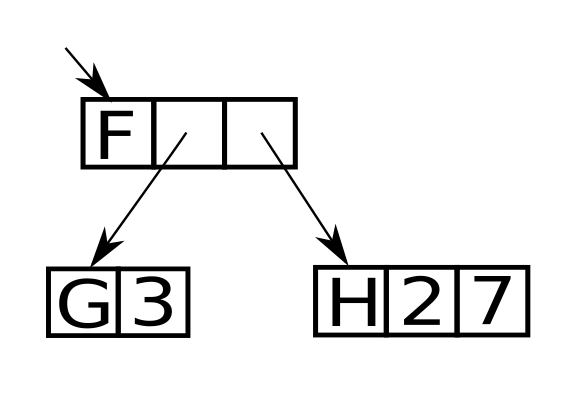
You could use a stack and push stack frames for “F”, “G”, and “H”. However, I wanted to experiment with another model, graph rewriting. Note that since we’re rewriting eagerly we’re rewriting the innermost expression first.
The evaluation strategy Egel uses shown below is extremely simplistic: Start with the node which is to be rewritten first, store the result where necessary -the dotted lines-, and continue with the next node to rewrite -the straight lines-.
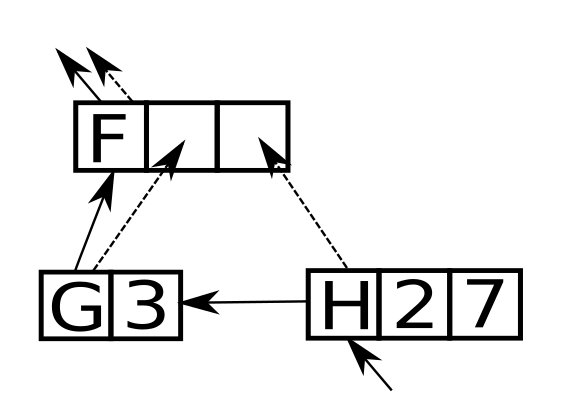
In this example, the node “H 2 7” is reduced first. Two things can happen: That node may reduce to a constant in which case the result is stored in the node of “F” and evaluation progresses with “G 3”. Or “H 2 7” requires more calculation, in which case the graph is expanded with the result of applying “H” to “2” and “7”.
That’s it. Note that the result is still a directed acyclic graph. That’s what enables me to implement Egel’s interpreter with native C++ reference counted pointers.
Note: For brevity the above pictures don’t completely correspond to the model coded in C++, where an OO hierarchy of nodes and arrays of pointers to nodes is used.
Invariants
The byte code generated by the Egel interpreter must maintain some properties. Being, a) the ‘stack’/’spine’ forms a directed acyclic graph and b) the results calculated are such graphs too.
Furthermore, no expression should be reduced twice.
Drawbacks
The method described is, of course, a slow and restrictive manner of evaluation.
- For one, stack based evaluators are often faster because pushing data to, or popping from, a stack is less computationally expensive than allocating, and deallocating, heap nodes.
- Also, it’s a term rewrite system so you can’t allow for assignment since that would usually allow you to create cyclic structures, though there are means to relax this restriction.
- In order to allow for a more expressive input language, a technique called lambda lifting is needed. That technique results in prohibitively slow code since it ‘recaptures’ variables in the context.
Advantages
The benefits of this model are fourfold.
- First, you don’t run out of stack space which is really important in a functional language as I have experienced, unfortunately. It’s a slow but extremely robust mode of operation.
- Second, it is still a tree rewrite system so there is no need to care about tail call optimization. That is, say for “fac 5” the node is rewritten to the nodes corresponding to “5 * fac 4”; i.e., in classical terms, the stack frame is dropped and replaced. Thus, naive factorial still takes O(n) space but a tail recursive one should take O(1). And, no, that doesn’t generalize to most other languages, it’s just an advantage of term rewriting.
- Third, since the semantics still rewrites trees, or directed acyclic graphs, you can implement it with nothing more than reference counting. In this case using C++’s shared pointers which has some additional benefits regarding predictable behavior, punctual disposing of resources, and concurrent evaluation.
- Fourth, the model allows for cheap concurrency where an extra process can be modeled by introducing not much more than an extra node which is rewritten concurrently. I.e., hardly bigger than a pointer. Since there is no stack the interpreter doesn’t need to instantiate one which should enable high scalability. It also allows for full sharing of graph nodes of other threads.
I like this model of evaluation, there isn’t much more to it. Some difficulties with this model are not discussed here.
Notes: Yes, what is shown are thunks or heap allocated stack frames. Yes, the thunks form a heapified stack but, dissimilar to standard stack based evaluation, stack frames are rewritten. No, code isn’t generated with a continuation passing style (CPS) transform though how the model was derived is much akin to that. Please note that CPS is a source-to-source transformation, whereas what is described here is an evaluation strategy. You need the latter first. Stated differently, the source code is translated directly to byte code for this model, and the model is the CPS transform of the term graph according to an eager semantics.
More: Egel also supports exception handling which is a natural extension of this model.